문제 링크
https://school.programmers.co.kr/learn/courses/30/lessons/12952?language=java
문제 이해하기
- 🔥 퀸은 가로,세로,대각선으로 이동할 수 있습니다.

그림1
퀸 하나를 내려 놓았을 경우 빨간색(가로,세로,대각선)에는 다른 퀸을 놓을 수 없습니다.
- 🔥 그러므로 한 행에는 반드시 하나의 퀸만 올 수 있습니다.

그림2
- 🔥 행렬은 반드시 $(n * n)$ 행렬입니다.
이 핵심들은 당연하게 보이지만 중요한 이유는 한 행에는 반드시 하나의 퀸만 올 수 있고,행과 열의 수가 같다면 2차원 배열로 풀지 않고 1차원 배열로도 풀 수 있습니다.
즉, 처리속도를 확 낮출 수 있다는 의미입니다.
- 🔥 대각선을 구하는 방법은
|기존 퀸의 행 - 배치할 퀸의 행| == |기존 퀸의 열 - 배치할 퀸의 열|이 성립하면 대각선에 있다고 봐야 합니다.

핵심4 예시
현재 퀸은 (0,2)와 (2,0)에 있습니다. 이 퀸은 서로 대각선에 위치합니다.
|0-2| == |2-0|는 성립하므로 두 퀸은 대각선에 위치합니다.
문제 풀이
코드-1
public class Solution {
public int solution(int n) {
int answer = 0;
for(int first=0; first<n; first++) {
int[] board = new int[n];
Arrays.fill(board, -1);
board[0] = first;
answer += checkPutTheQueenAll(board, n, 1);
}
return answer;
}
public int checkPutTheQueenAll(int[] board, int n, int row) {
if(row == n) return 1;
int count = 0;
for(int col=0; col<n; col++) {
boolean checkPut = true;
for(int pick=0; pick<row; pick++) {
if(col == board[pick] || row-pick == Math.abs(col-board[pick])) {
checkPut = false;
break;
}
}
if(checkPut) {
board[row] = col;
count += checkPutTheQueenAll(board, n, row+1);
}
}
return count;
}
}기본적으로 머리로는 이해하고 있어야 할 구조는 2차원배열을 쓴다는 거예요.
근데 어차피
board[0] = 0 을 2차원 배열로 보면 (0,0) 에 퀸이 있는 상태입니다.board[0] = 2 이면 (0,2)에 퀸이 있는 상태이구요.
n=4일 경우 첫 번째 퀸의 위치가 정해지는 경우의 수는 몇일까요?
답은 4입니다.
(0,0) (0,1) (0,2) (0,3) 첫 번째 퀸의 위치는 한 행의 모든 열에 올 수 있어요.
그리고 첫 번째 퀸의 위치에 따라 두 번째, 세 번째, 네 번째 행에 퀸이 어디에 오느냐가 달라지죠.
그러므로 우선적으로 고려해야할 부분은
그 코드가 아래 코드1번 이구요.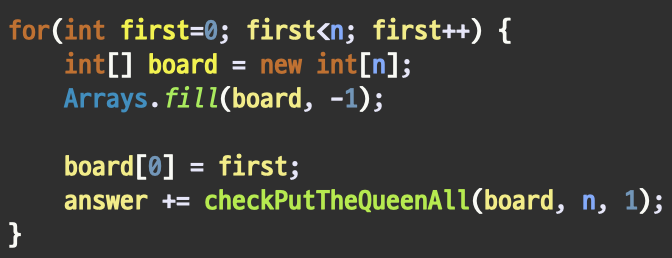

그림3의 퀸의 위치를 보면 첫 번째 퀸이 (0,0)일 경우
두 번째 퀸은 (1,2) 일 수도 있고, (1,3)일 수도 있어요.
그러므로 이 부분은 재귀로 풀어야 해요.
(1,2)에 퀸을 놓았을 경우 다음 행의 퀸을 놓을 위치와(1,3)에 퀸을 놓았을 경우 다음 행의 퀸을 놓을 위치가 달라지기 때문이에요.
그러므로 (1,2)에 퀸을 놓았다고 가정하고 정답을 찾는 방향과(1,3)에 퀸을 놓았다고 가정하고 정답을 찾는 방향
이런 식으로 모든 경우의 수를 생각해야 한답니다.
조금 더 이해를 돕기 위해 (1,2)에 퀸을 놓았을 경우와 (1,3)에 퀸을 놓았을 경우를 그림으로 볼게요.
(1,2)에 퀸을 놓았을 경우

그림4 - (1,2)
그림에서 보다시피 3번행에 놓을 수 있는 퀸이 없어요. 그러므로 배치불가입니다.
(1,3)에 퀸을 놓았을 경우

그림5 - (1,3)
3번행에 퀸을 놓았지만, 4번행에 퀸을 놓을 수 없어 이 경우에도 배치불가입니다.
이렇게모든 경우의 수를 탐색하며 마지막 행에 퀸을 놓았을 때에는 모든 퀸을 배치했다고 판단 합니다.
그 함수가 바로checkPutTheQueenAll입니다.
퀸을 놓을 수 없는 위치만 판단하고 퀸을 놓을 수 없으면 종료, 퀸을 놓을 수 있으면 다음 퀸의 위치를 찾는 방식으로 재귀를 진행하면 됩니다.
테스트 케이스 처리속도
| 테스트 번호 | 결과 (시간) |
|---|---|
| 테스트 1 〉 | 통과 (0.02ms, 71.4MB) |
| 테스트 2 〉 | 통과 (0.03ms, 73.3MB) |
| 테스트 3 〉 | 통과 (0.03ms, 71.8MB) |
| 테스트 4 〉 | 통과 (0.06ms, 76.3MB) |
| 테스트 5 〉 | 통과 (0.19ms, 77.7MB) |
| 테스트 6 〉 | 통과 (0.56ms, 88.1MB) |
| 테스트 7 〉 | 통과 (0.98ms, 85MB) |
| 테스트 8 〉 | 통과 (2.51ms, 70.3MB) |
| 테스트 9 〉 | 통과 (8.08ms, 78.2MB) |
| 테스트 10 〉 | 통과 (26.92ms, 83.6MB) |
| 테스트 11 〉 | 통과 (136.51ms, 100MB) |
'Algorithm > Java' 카테고리의 다른 글
| 프로그래머스 - 최솟값 만들기 JAVA :: 12941 (0) | 2022.08.01 |
|---|---|
| 프로그래머스 - 양궁대회 JAVA :: 2022 KAKAO BLIND RECRUITMENT :: 92342 (0) | 2022.07.27 |
| 프로그래머스 - 행렬의 곱셈 java (0) | 2022.07.15 |
| 프로그래머스 - 피보나치 수 java :: 모듈로 연산 (0) | 2022.07.15 |
| 프로그래머스 - 하노이의 탑 java (재귀/반복문) :: 12946 (0) | 2022.07.13 |